Local Vibrational Mode Theory
The local vibrational mode theory was originally developed by Konkoli and Cremer in 1998 [1-4] and it describes the theoretical adiabatic internal modes (later known as local vibrational modes) derived from the experimentally measurable normal vibrational modes [5] in molecular structures by solving the mass-decoupled Euler–Lagrange equations.
A local vibrational mode associated with an internal coordinate parameter \(q_n\) is defined as the infinitesimal displacement of this internal coordinate, followed by the relaxation of all other atoms in this molecular structure.
Like normal vibrational modes having their corresponding frequencies and force constants, a local vibrational mode has its local mode force constant \(k_n^a\) (also known as relaxed force constant) and frequency \(\omega_n^a\). For the local vibrational mode associated with a bond length, the local mode force constant corresponds to the local stretching force constant describes the intrinsic strength of this chemical bond of interest. \(k_n^a\) as a unique measure of bond strength as an alternative to the bond (dissociation) energy of covalent bond or binding energy of non-covalent interaction has its advantages over the latter bond strength measure.
In 2019, the local vibrational mode theory was extended from molecular systems to periodic systems of one through three dimensions (1-3D) in periodicity [6]. The local vibrational mode associated with an internal coordinate \(q_n\) is defined as the vibration driven by this internal coordinate in all primitive cells while relaxing all other parts of the periodic system. This theoretical extension enables the quantification of chemical bond strengths in solids and molecules in a head-to-head fashion.
So far, the local vibrational mode theory as a powerful tool has been applied to study both covalent bonds and non-covalent interactions including hydrogen, halogen, pnicogen, chalcogen and tetrel bonding. Interested readers may check a review article by Kraka et al. [7].
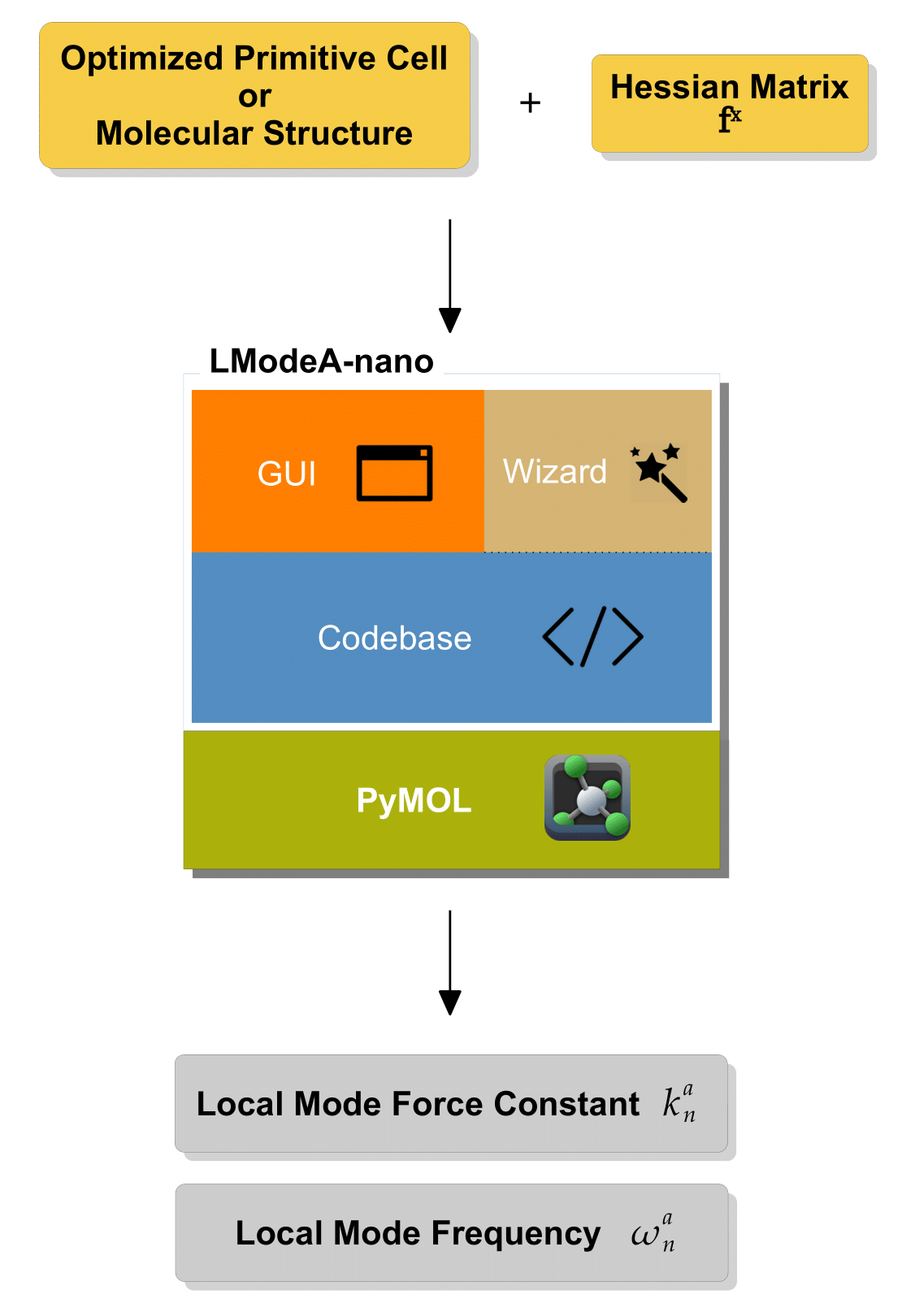
Necessary input information needed for calculating the local vibrational modes in molecules or solids includes
optimized molecular structure or primitive cell structure
Hessian matrix corresponding to the optimized structure
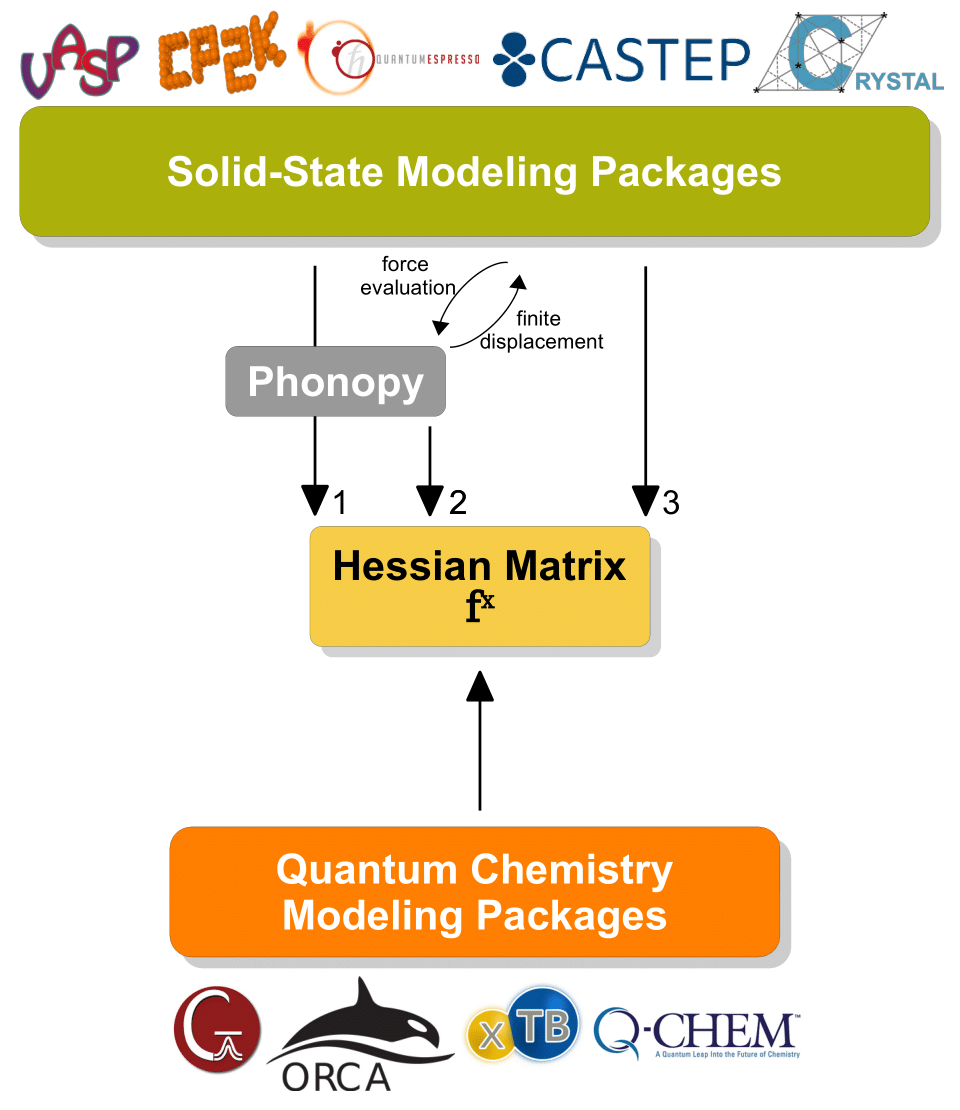
Hessian matrix collecting the second-order energy derivatives with regard to Cartesian coordinates is necessary for vibrational frequency calculations in molecules and solids.
Next, tutorials will be given on how to use LModeA-nano with the input data generated by solid-state and quantum chemistry modeling packages.
References
Konkoli, D. Cremer, A New Way of Analyzing Vibrational Spectra. I. Derivation of Adiabatic Internal Modes, Int. J. Quantum Chem. 67, 1 (1998) 📎
Konkoli, J. A. Larsson, D. Cremer, A New Way of Analyzing Vibrational Spectra. II. Comparison of Internal Mode Frequencies, Int. J. Quantum Chem. 67, 11 (1998) 📎
Konkoli, D. Cremer, A New Way of Analyzing Vibrational Spectra. III. Characterization of Normal Vibrational Modes in terms of Internal Vibrational Modes, Int. J. Quantum Chem. 67, 29 (1998) 📎
Konkoli, J. A. Larsson, D. Cremer, A New Way of Analyzing Vibrational Spectra. IV. Application and Testing of Adiabatic Modes within the Concept of the Characterization of Normal Modes, Int. J. Quantum Chem. 67, 41 (1998) 📎
Wilson, J. C. Decius, P. C. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications: Mineola, NY (2012)
Tao, W. Zou, D. Sethio, et al., In Situ Measure of Intrinsic Bond Strength in Crystalline Structures: Local Vibrational Mode Theory for Periodic Systems, J. Chem. Theory Comput. 15, 1761 (2019) 📎
Kraka, W. Zou, Y. Tao, Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory, WIREs: Comput. Mol. Sci. 10, e1480 (2020) 📎